- Home
- Dome Kits for Sale
- Manuals
- Videos
- Dome Calculators
- 2V Dome Calculator
- 3v 3/8 Dome Calculator
- 3v 5/8 Dome Calculator
- 4v Dome Calculator
- 5v 7/15 Dome Calculator
- 5v 8/15 Dome Calculator
- 6v Dome Calculator
- 2v Silo Domes
- Tunnel Domes
- Tunnel Dome 0 Ext.
- Tunnel Dome 1 Ext.
- Tunnel Dome 2 Ext.
- Tunnel Dome 3 Ext.
- Tunnel Dome 4 Ext.
- Tunnel Dome 5 Ext.
- Tunnel Dome 6 Ext.
- Tunnel Dome 7 Ext.
- Tunnel Dome 8 Ext.
- Tunnel Dome 9 Ext.
- Tunnel Dome 10 Ext.
- Tunnel Dome 11 Ext.
- Tunnel Dome 12 Ext.
- Tunnel Dome 13 Ext.
- Tunnel Dome 14 Ext.
- Tunnel Dome 15 Ext.
- Tunnel Dome 16 Ext.
- Tunnel Dome 17 Ext.
- Tunnel Dome 18 Ext.
- Tunnel Dome 19 Ext.
- Tunnel Dome 20 Ext.
- Geodesic Spheres
- Octahedron Domes
- Alternative Domes
- Contact Us

Zip Tie Domes™
Geodesic Dome Kits that are Easy to Build!
Geodesic Dome Greenhouse Kits and Chicken Coop Kits For Sale
Zip Tie Domes™


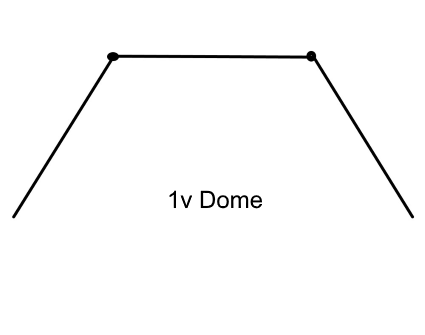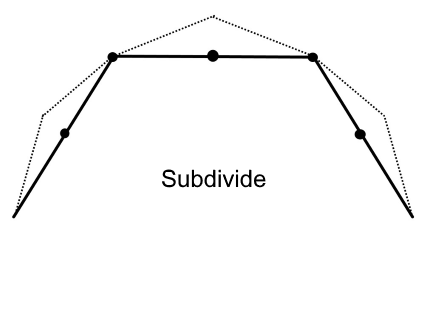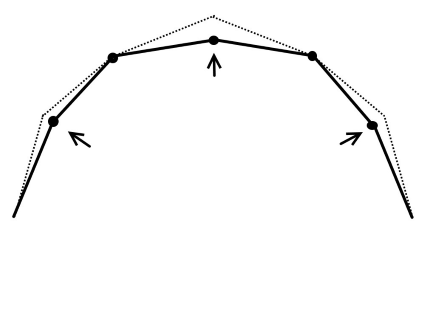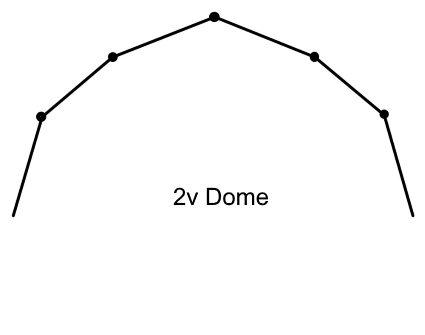
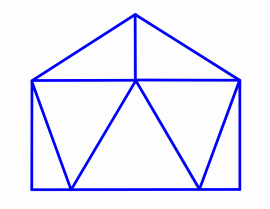 1v Dome
1v Dome
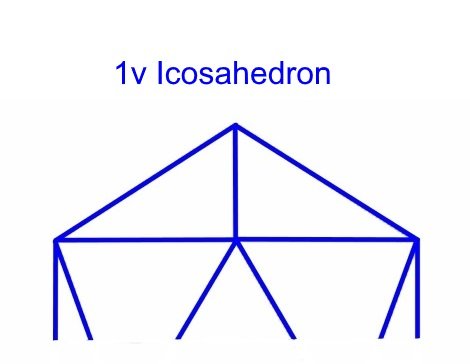
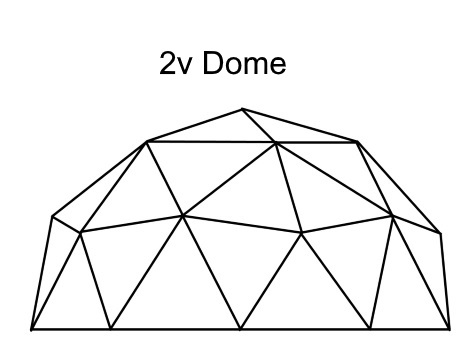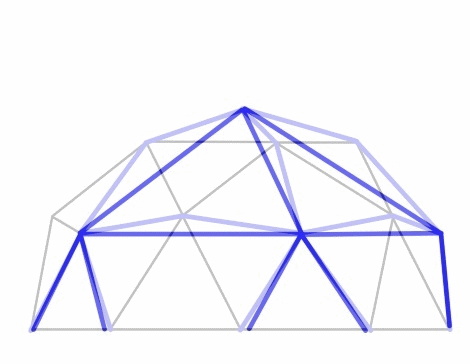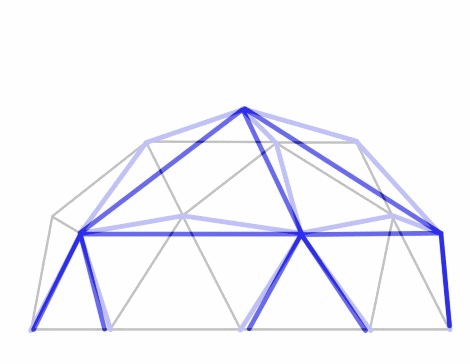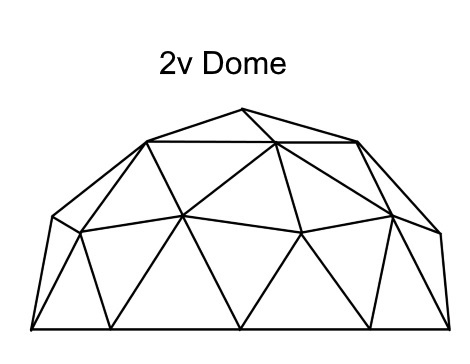
 2v Dome
2v Dome
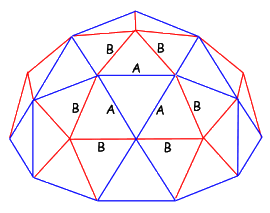
 3v Dome
3v Dome
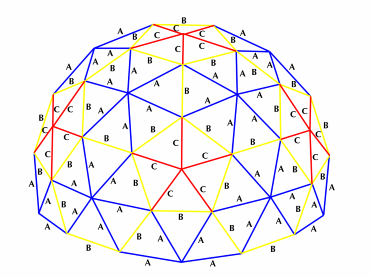
 4v Dome
4v Dome
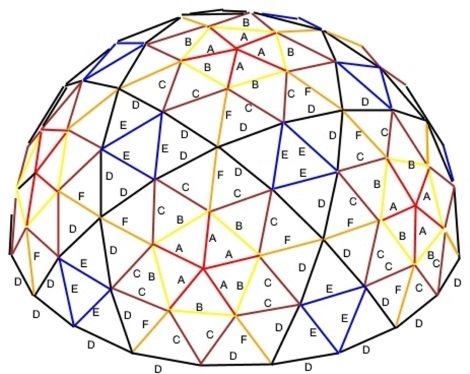
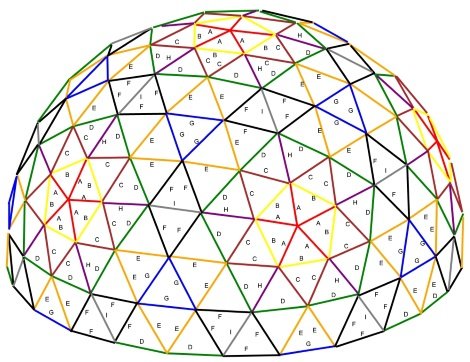 5v Dome
5v Dome
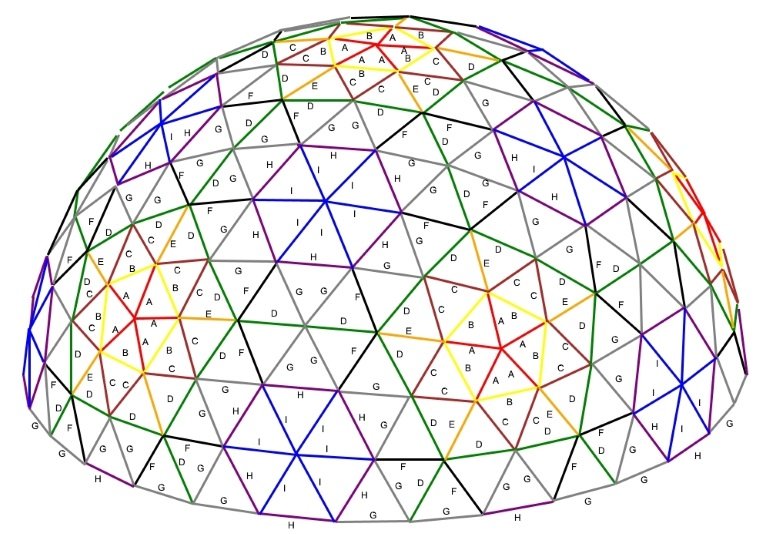 6v Dome
6v Dome







 Dodecahedron
Dodecahedron
 Octahedron
Octahedron
 Tetrahedron
Tetrahedron
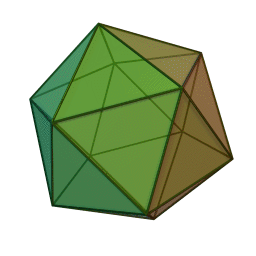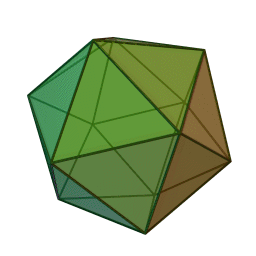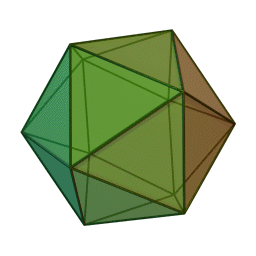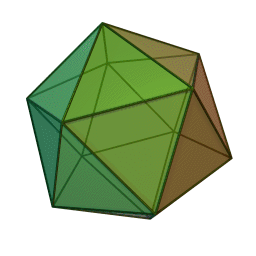
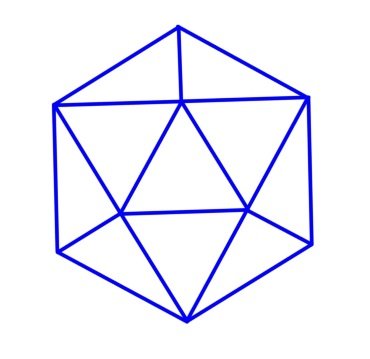
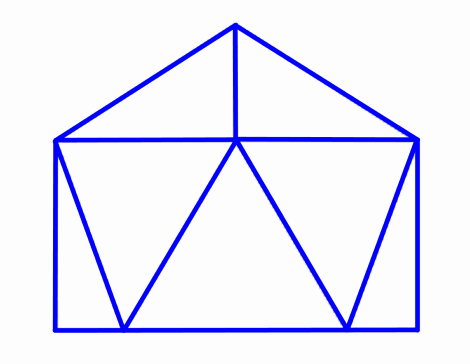

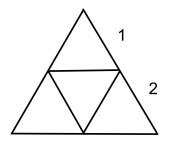
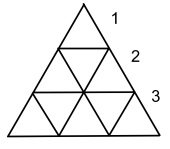
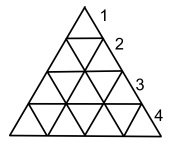
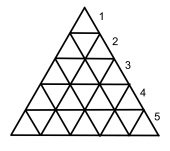
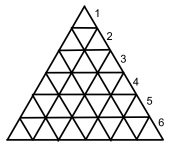
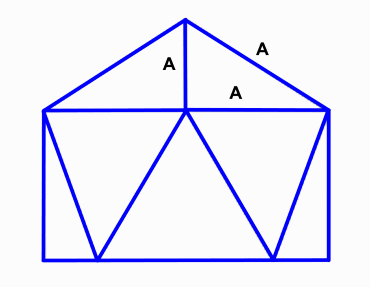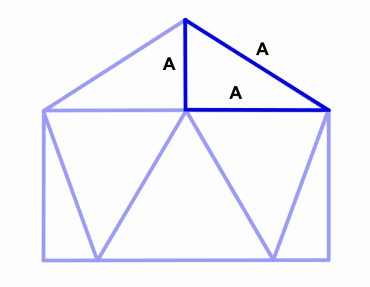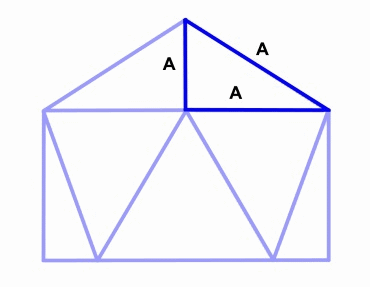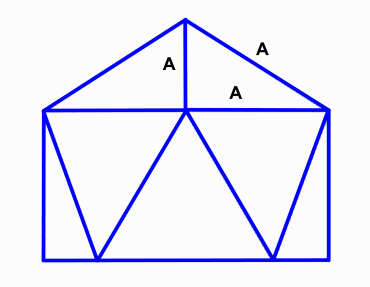
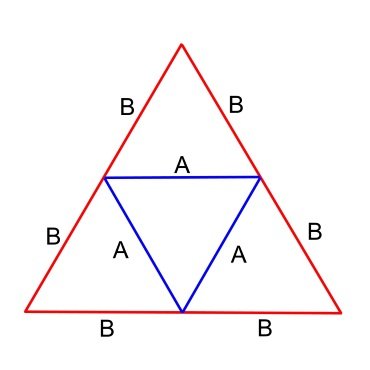






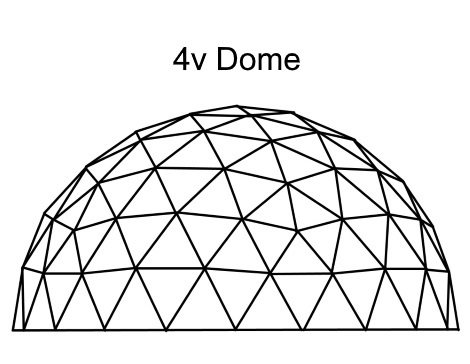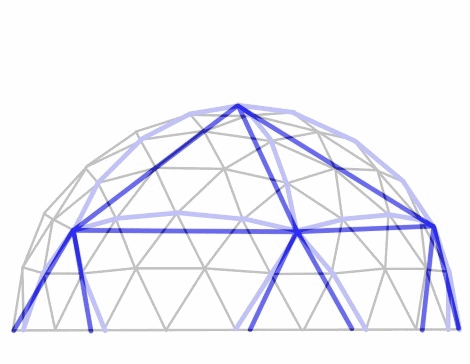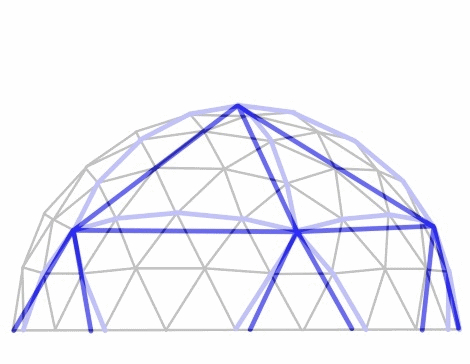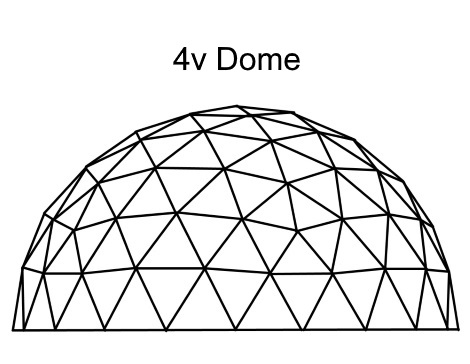


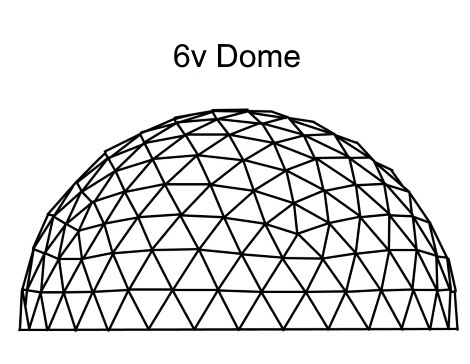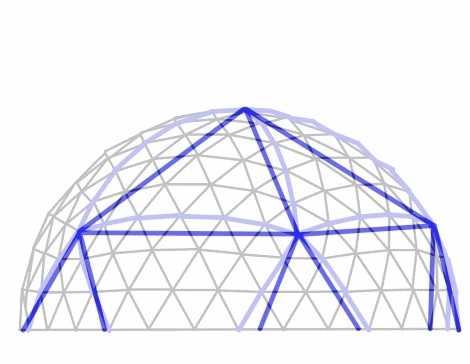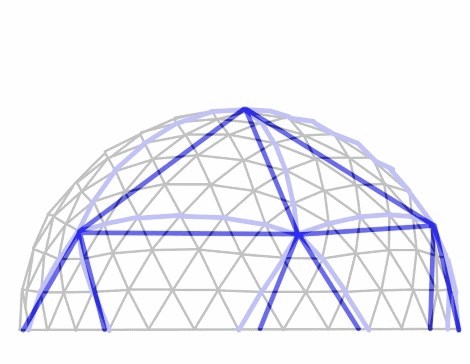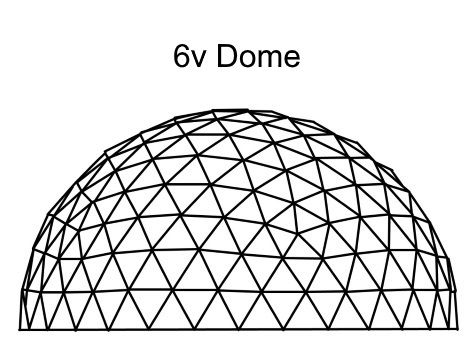
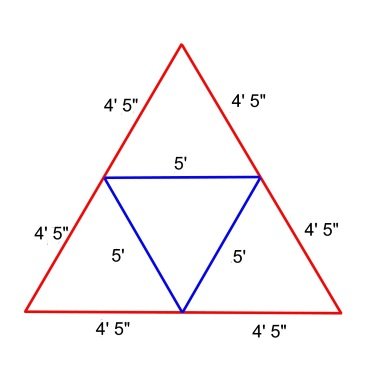
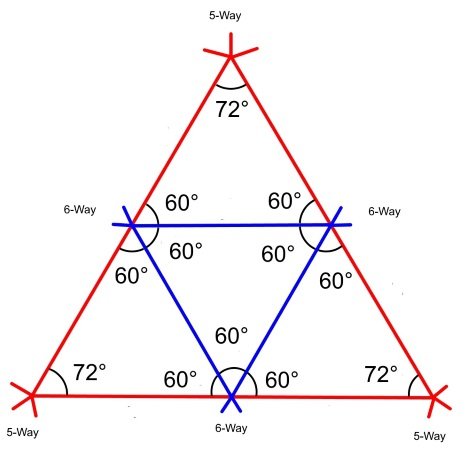
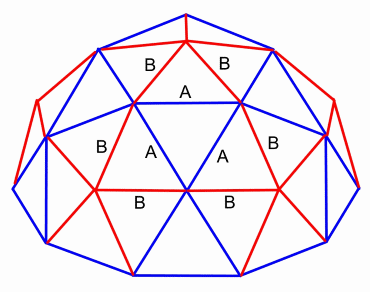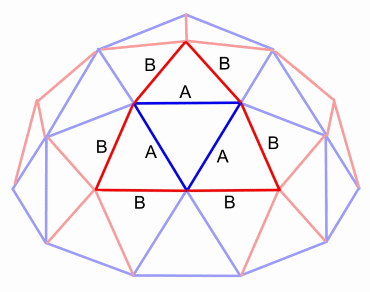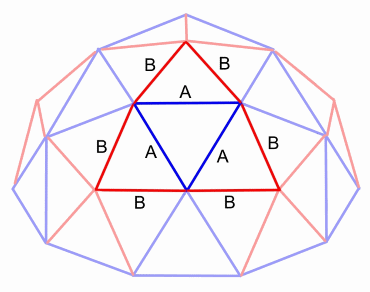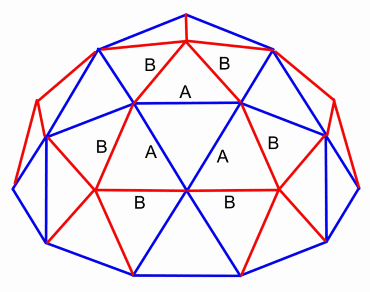

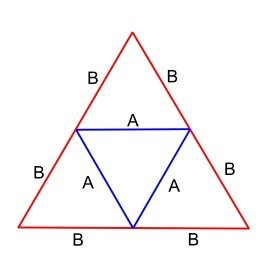
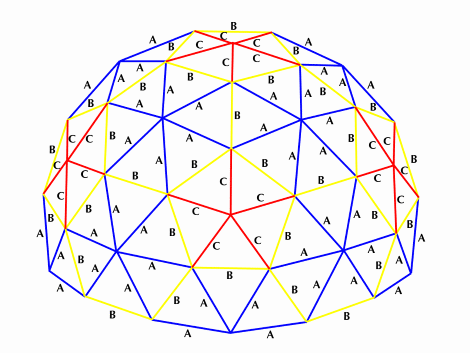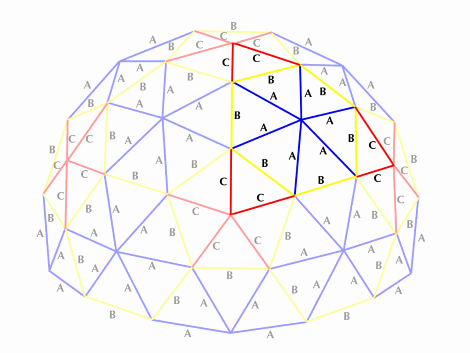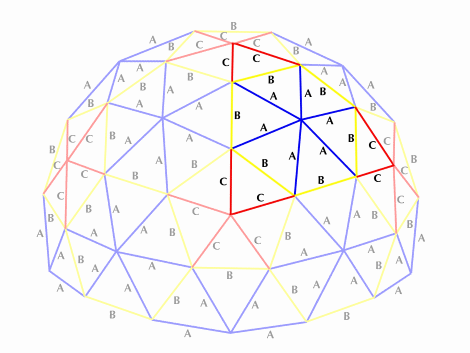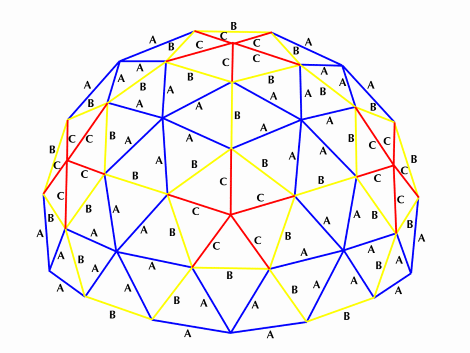
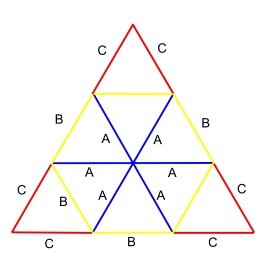
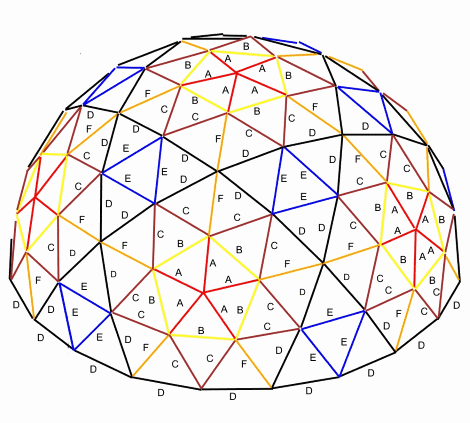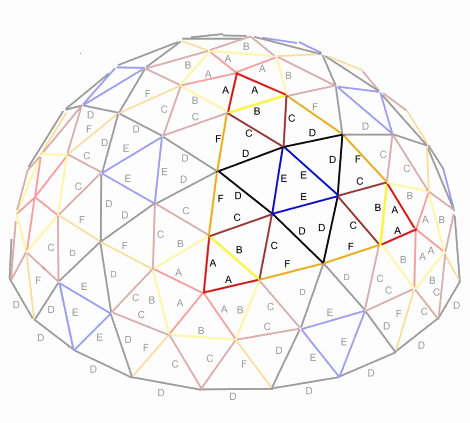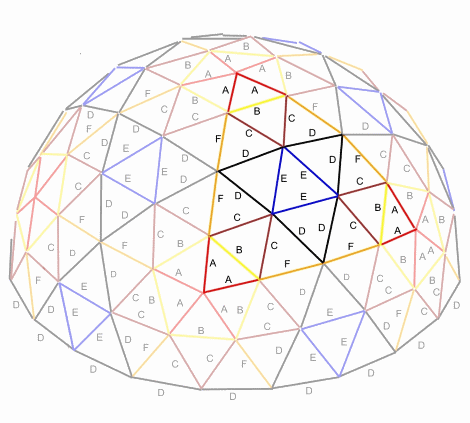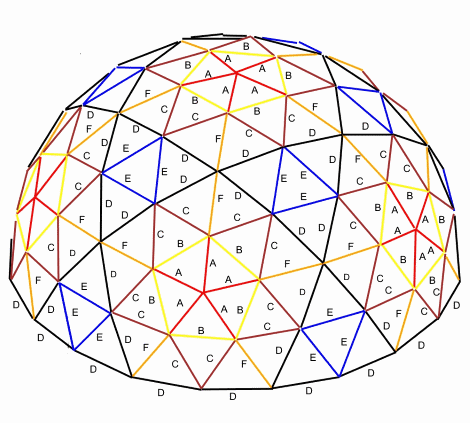
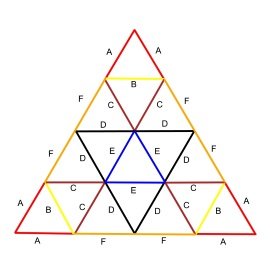
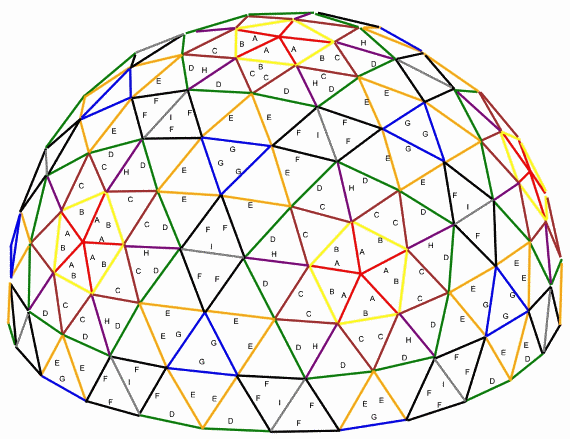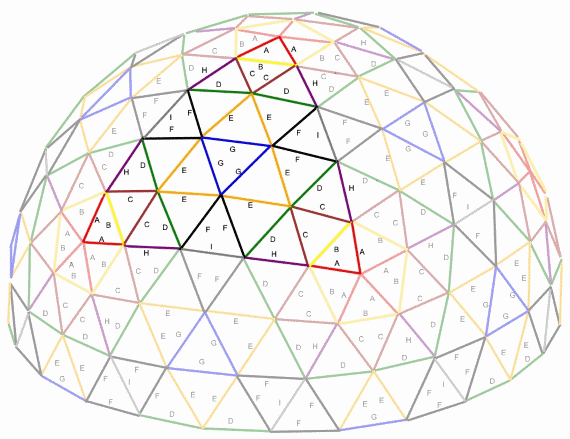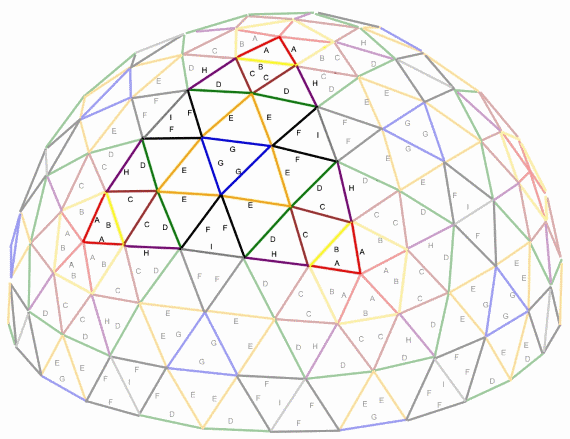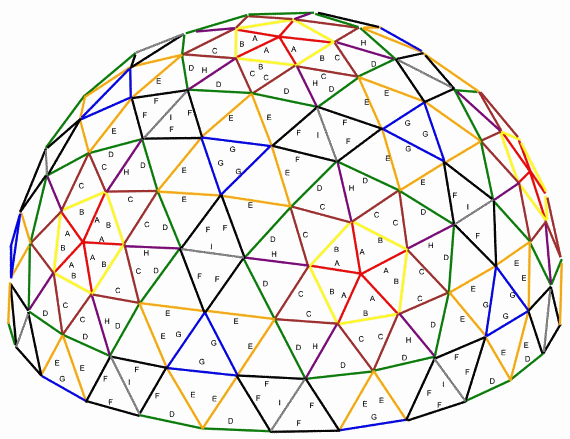
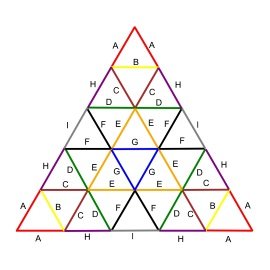
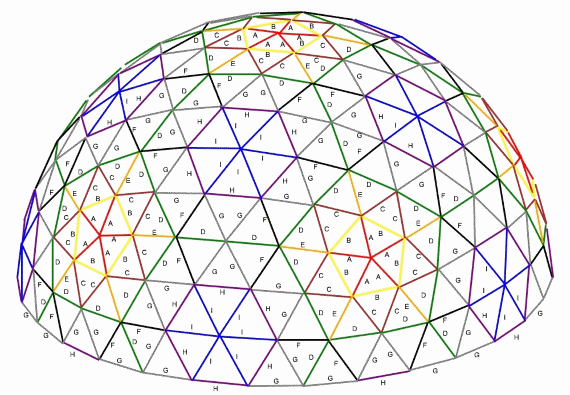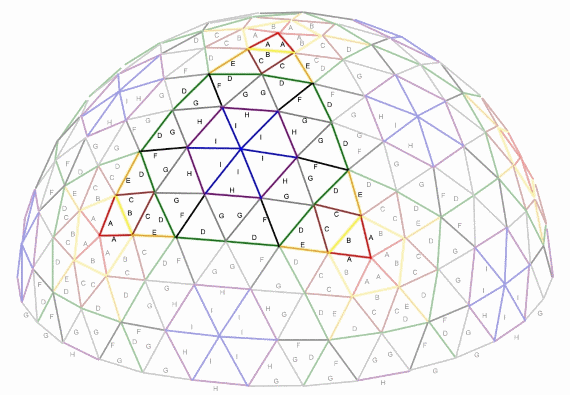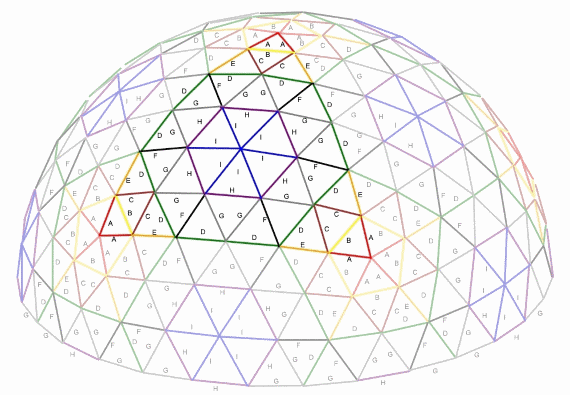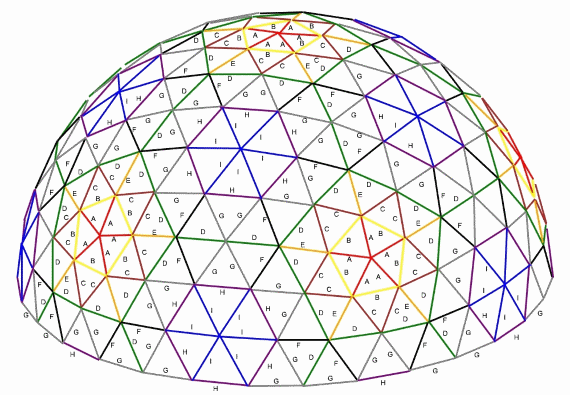
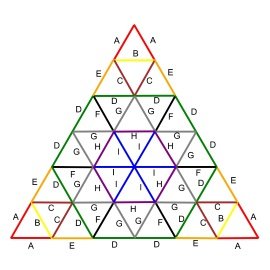

 3v Dome
3v Dome
 4v Dome
4v Dome
 5v Dome
5v Dome
 6v Dome
6v Dome




